Neural Turing Machine(NTC) 和 Differentiable Neural Machine(DNC) 的相关笔记。
涉及论文:
- Neural Turing Machine
Neural Turing Machine(2014) - Differentiable Neural Machine
Hybrid computing using a neural network with dynamic external memory (2016)
Introduction
当今所有的计算机体系都源自冯诺依曼体系(Von Neumann, 1945),三大要素:
- elementary operations
基本操作,如加减乘除 - logical flow control (branching)
逻辑流程控制,如 if-else-then, for, while - external memory
外部存储器,内存和硬盘
RNN 被认为是 Turing-complete 的,理论上可以拟合任何函数,有模拟流程的能力,然而理论上可以,实际实现并没有那么简单。NTM/DNC 的重点是 存储管理,它能够通过一个大的、可寻址的外部存储器来扩展标准 RNN 能力,大大简化算数等任务。
Turing Machine
NTM/DNC 的灵感来自于图灵机。图灵机就是一种简单的计算机模型,摘一段概念:
A Turing machine is a simple model of the computer. Like modern computers, it encapsulates the idea of having an external memory as well as some sort of processor. Essentially, a Turing machine consists of a tape with instructions written on it and the device that can read up and down the tape. Based on what it reads on the tape, it can decide to move in a different direction to write a new symbol or erase a symbol, and so on.
很简单,由 外部存储器(写有指令的磁带)和存储器(能够沿着磁带读取的设备) 组成,根据磁带上读取到的指令,计算机能够决定在磁带上不同的方向上移动来进行写入或者擦除新符号等操作。
神经图灵机的灵感就来自图灵机的架构,也有 控制器(神经网络)和外部存储器(memory) 构成,试图去解决一些计算机能够解决的很好但机器学习模型很难解决的问题,比如说算法,或者说上面提到的冯诺依曼体系的一些要素。
NTM/DNC vs. TM
NTM/DNC 灵感来自于 TM,最关键的区别是神经图灵机是 可微分的(differentiable) 图灵机。计算机/图灵机的计算是绝对的,要么是 0 要么是 1,计算机在非此即彼的逻辑或者整数中运作。然而大多数的神经网络和机器学习更多会使用实数,使用更平滑的曲线,这样会更容易训练(如 BP,可以通过输出追踪回去调整参数以得到希望的输出)。神经图灵机采用基本的图灵机思想,但同时找到了平滑的模拟函数,也就是说,在图灵机磁带上,神经图灵机 NTM 可以决定“稍微”向左或者向右移动,而不是单纯的向左跳一个或者向右跳一个。
Application
- Learn simple algorithms(Copy, repeat, recognize simple formal languages)
能够学习简单的算法(夸张一点,本质上就是尝试着取代程序员)
NTM/DNC 能够接受输入和输出,并且学习得到能够从输入映射到输出的算法
如说复制任务,它能够学会接受相对短的序列,并重复几次。这让 LSTM 来做它就会崩溃,因为 LSTM 并不是在学习算法,而是试图一次性解决一个整体问题,它意识不到前两次所做的事情就是它们之后应该做的
再比如说识别平衡的括号,这涉及到了栈(stack)的算法,NTM/DNC 可以像程序员一样完成这个任务 - Generalize
NTM/DNC 的计算图是对所有任务通用的 - Do well at language modeling
擅长语言建模
比如做完型填空,能够猜测一个单词在句子或者文档语境中的意思 - Do well at bAbI
擅长推理
在 bAbI 数据集上效果很好
Problems
- Architecture dependent
实现的时候需要谨慎做出如对每一时刻的输入能读取/写入多少向量这类的决策,否则很有可能永远都得不到一个合理的结果 - Large number of parameters
参数量非常大 => RAM 压力很大 - Dosen’t benefit much from GPU acceleration
序列输入,每一步输入都依赖之前的输入,也就很难并行化,不能受益于 GPU 加速 => 很难训练
很难训练还表现在:
- Numerical Instability
数值不稳定性。在试图学习算法时会更倾向于犯大错误,而如果在算法中犯了一个错误,所有的输出结果都会是不正确的。换言之,训练时神经图灵机总是很难找到需要的算法 - Using memory is hard
大量数据+足够时间,大多数神经网络都会得到一些结果,而神经图灵机经常会卡住,它们经常一遍又一遍地一味地产生那些经常重复的值
因为使用记忆是很困难的,不仅要学会记住之后解决问题需要的东西,还不能意外的忘记它 - Need smart optimization
1+2 => 需要很好的优化
如 gradient clipping, loss clipping, RMSprop, Adam, try different initialization, curriculum learning…
上面这些问题会让神经图灵机很难在实际中应用。
NTM/DNC vs. MemNN
异:
DNC 侧重记忆管理。MemNN 侧重 memory 查询,在记忆管理上非常简单,一般以 QA 为例,就是每句话 encode 成 vector,然后保存下来,所谓的更新大多是把不重要的 memory 清出去空个位出来给新的 memory。而 DNC 花更多努力在记忆管理上,注重更新 memory 和 memory 的时间关系,包含更多的操作,更新、删除、添加等。
另外,NTM/DNC 侧重算法任务,能够自动从数据中学习算法,而一般而言 MemNN 侧重的是 QA 任务。
同:
都是从 model architecture 层面,将多个 machine learning model 联合起来处理复杂的任务,比如 LSTM 通常是来处理线性数据,MemNN/NTM 可能包含多个 LSTM,能够处理多个线性结构(类似图结构)
Neural Turing Machines(NTM)
Basic Idea
主要创新是将神经网络与外部存储器(external memory)结合来扩展神经网络的能力(通过注意力机制进行交互),可以类比图灵机,不过 NTM 是端到端可微的,所以可以使用梯度下降进行高效训练。
两个 主要元件 是 controller 和 memory bank。类比计算机来看 基本思路,实际是把神经网络看成是 CPU,把 memory 看做是计算机内存。CPU 根据任务来确定到内存的哪个位置读写信息,不过计算机的内存位置是离散数据,而 NTM 里是连续可导的。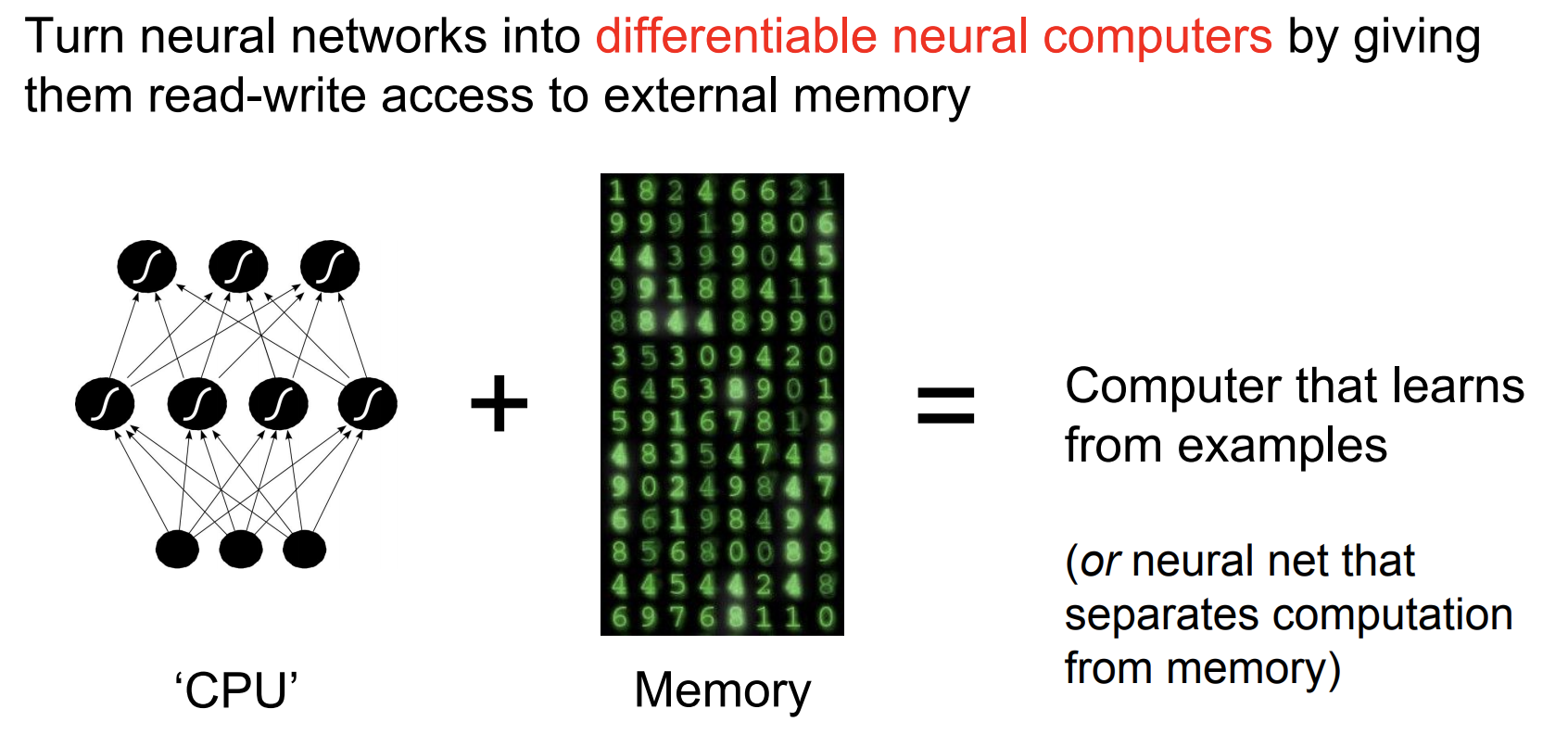
Architecture
一张图读懂架构,取 DeepMind DNC Slides 做了部分修改。最重要的概念还是那句话,每个组件都是可微分的,所有操作皆可导,这就可以直接用梯度下降训练来训练。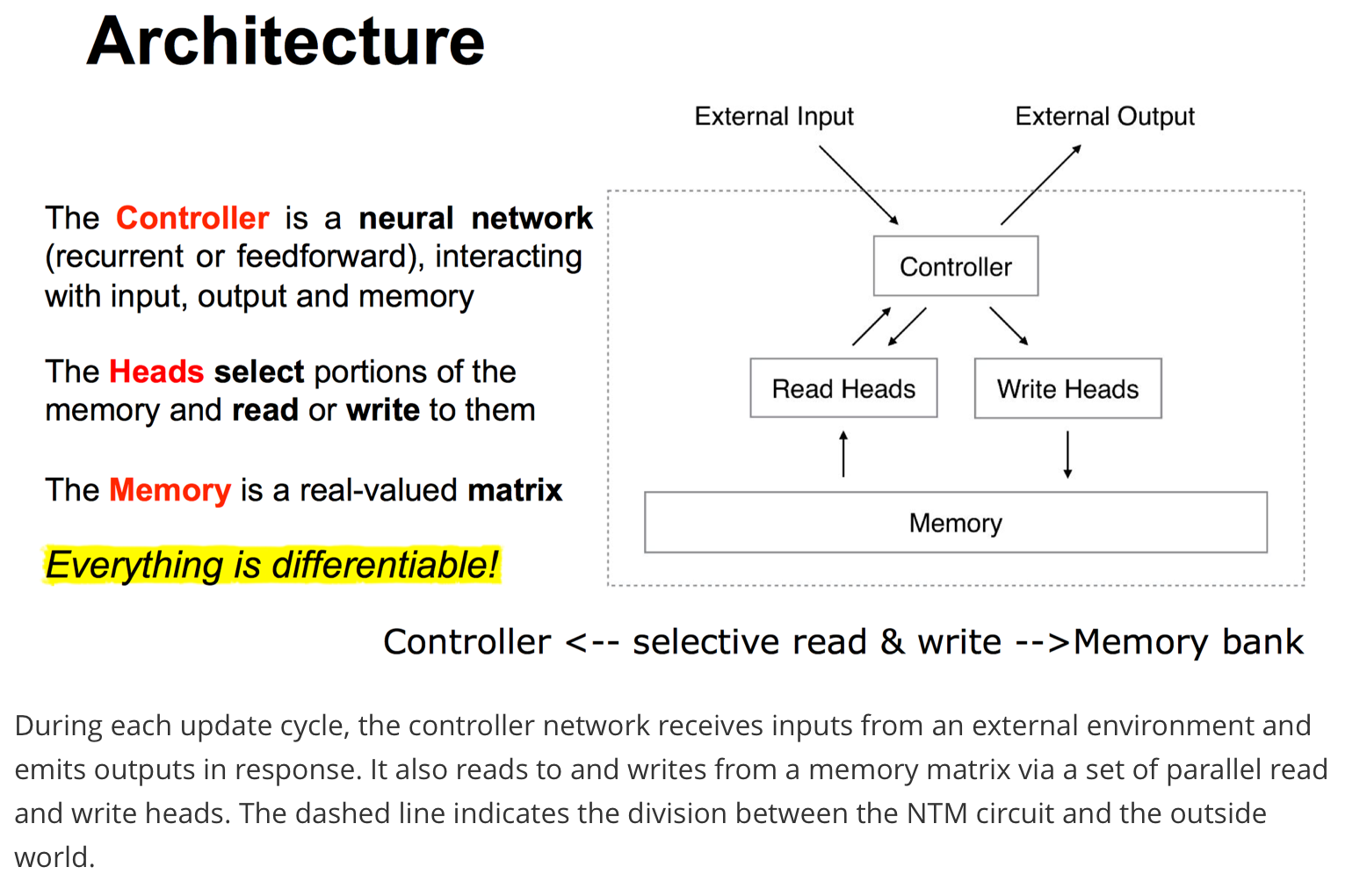
主要来研究读写操作。
Read Heads
读操作和普通的 MemNN 相似,使用 attention 原理计算每个 memory vector 的权重向量,然后对 memory vector 进行加权生成读操作的结果。
$$r_t \leftarrow \sum^N_{i=1} w_t(i)M_t(i)$$
$M_t$ 是一个 NxM 的矩阵,表示 t 时刻的 memory,N 是 memory 的数量,M 是 memory vector 的维度。$w_t$是 t 时刻产生的权重向量,和 memory 数量相同,进行了归一化,$\sum_iw_t(i)=1, \ \ 0 \le w_t(i) \le 1, \forall i$
Write Heads
Erase and Add
写操作包含两个步骤:先擦除(erase) 后添加(add)
- Erase
input + controller 产生 erase vector $e_t \in R^M$, $e_t(d) \in (0,1)$
input + memory 产生 $M_t^{erased}(i) \leftarrow M_{t-1}(i)[1-w_t(i)e_t]$
和读操作一样,需要由 attention 机制得到 weight vector,表示每个 memory vector 被改动的幅度的大小,有多少个 memory 就有多少个 $w_t$
将上一时刻每个 memory vector 都乘上一个 0-1 之间的 vector,就是擦除操作,相当于 forget gate
如果 $w_t$ 和 $e_t$ 都为 1,memory 就会被重置为 0,如果两者有一个为 0,那么 memory 保持不变。多个 erase 操作可以以任意顺序叠加 - Add
input + controller 产生 add vector $a_t \in R^M$ ,$a_t(d) \in (0,1)$
input + memory 产生 $M_t(i) \leftarrow M_t^{erased}(i) + w_t(i)a_t$
相当于 update gate
同样的,多个 add 操作的顺序并没有关系
所有的 memory vector 共享 $e_t, \ a_t$,erase 和 add 操作中的 $w_t$ 也是共享的。再次注意 erase vector 和 add vector 都是由 controller 对 input 做编码得到的。
擦除和添加动作都有 M 个独立的 component,使得对每个 memory location 的修改可以在更细的粒度上进行。
Addressing
知道了怎么读写,现在来看看权重是如何产生的。主要通过两种方式来进行寻址,一是 content-based addressing,基于 controller 提供的状态向量 key vector 和当前 memory vector 的相似度来决定对内存地址的聚焦程度,另一个是 location-based addressing,通过地址来寻址,可能还会伴随权重的位移(rotational shift)。
整个 Addressing 过程的流程图: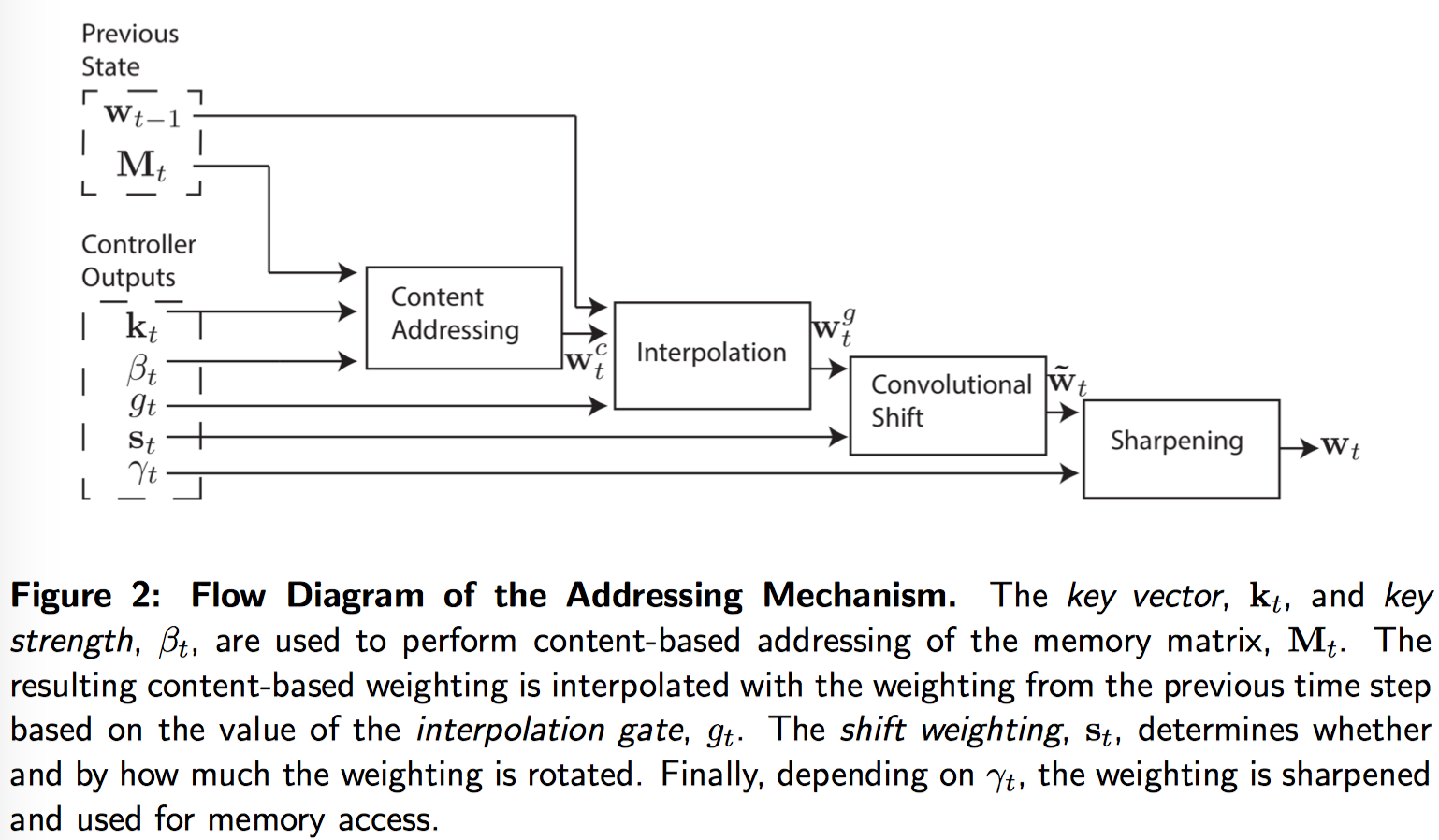
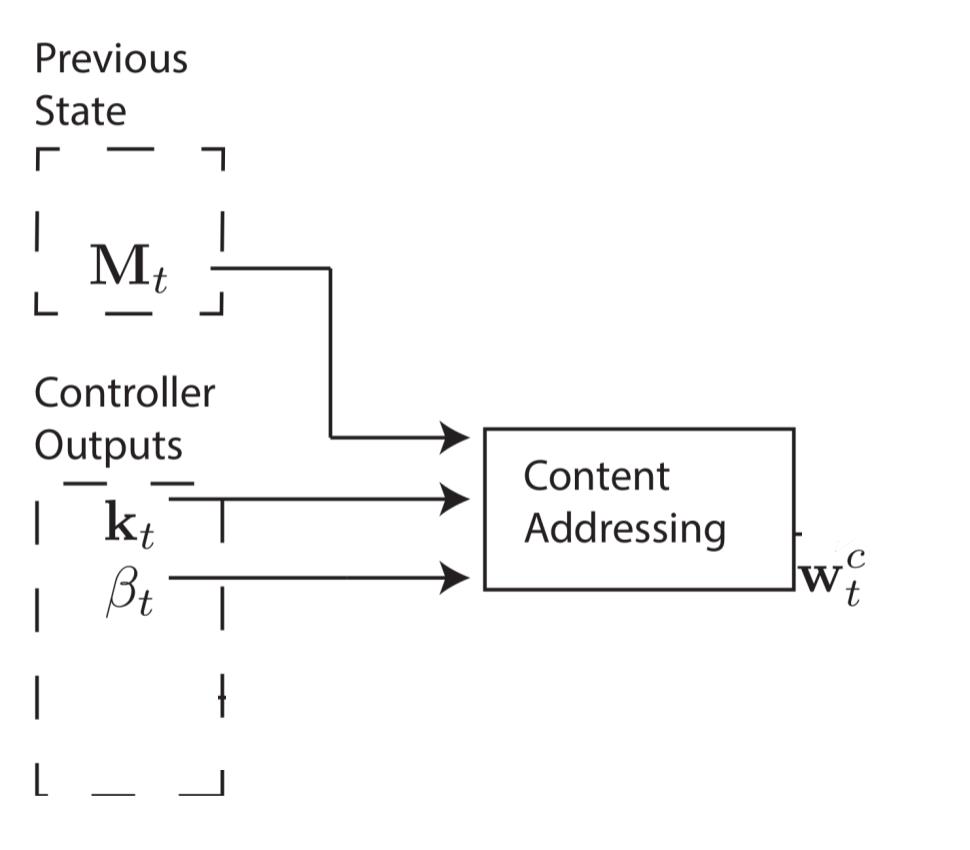
Content-based addressing
Controller 会产生一个长度为 M 的状态向量 key vector $k_t$,基于每一个 memory vector $M_t(i)$ 和 controller 状态向量 $k_t$ 的相似程度 K[·,·],计算每个 memory vector 的 attention 权重。其中相似度可以用 cosine similarity 计算,$K(u,v)={u v \over ||u|| ||v||}$
使用 softmax 将相似度转化为概率分布:
$$w^c_t(i) \leftarrow {exp(\beta_tK[k_t, M_t(i)]) \over \sum_j exp(\beta_tK[k_t, M_t(j)])}$$
其中,$\beta_t$ 可以放大或减弱聚焦的程度。$\beta_t=1$ 时就是标准的 softmax,而 $\beta$ 的值越大,越会强化最大相似度分数的 memory vector 的优势,可以看做赢者通吃。要注意的是 $\beta$ 不是超参数,而是 controller 预测得到的。举个具体的例子,在对话领域,如果输入时“呵呵”这类没有太多信息量的句子,那么 controller 就会产生一个非常接近 0 的 $\beta$,表示没有明确倾向去访问某个特定的信息;反之,如果是包含很多信息的输入,产生的 $\beta$ 值会很大。
content addressing 完成的下面一个流程,$k_t$ 可以看做是 controller 对输入进行编码产生的状态向量,$\beta_t$ 是标量,一个 concentration 参数。
Location-based addressing
不是所有的问题都可以通过 content-based addressing 来解决的。在一些特定任务尤其是有 variable-binding 的任务中,变量的内容是任意的,但变量还是需要一个可识别的名字/地址来 refer。比如说算数任务,x, y 代表任意值,要计算 $f(x,y)=x * y$,这时候 controller 就会把 x,y 存到对应的地址上,然后通过地址而不是数值内容来获取它们并进行乘法操作。
Content-based addressing 比 location-based addressing 更为通用,因为 Content-based addressing 本身可能包含地址信息。然而 location-based addressing 对某些形式的通用化很有必要,所以论文同时引入了两种寻址机制。
1. Interpolation Gate
第一步要进行插值计算。
$$w_t^g \leftarrow g_tw^c_t + (1-g_t)w_{t-1}$$
基于内容的 weight vector $w^c_t$ 和上一个时间的 weight vector $w_{t-1}$ 的线性组合,线性组合的参数 $g_t$ 是一个 (0, 1)之间的标量,由 controller 产生,表示多大程度上使用当前时刻基于内容的寻址,多大程度上使用上一时刻产生的 $w_{t-1}$
如果 g=0,那么 content-weighting 整个就被忽略了,只用上一时刻的权重;如果 g=1,那么上一时刻的权重就被忽略了,只使用 content-based addressing。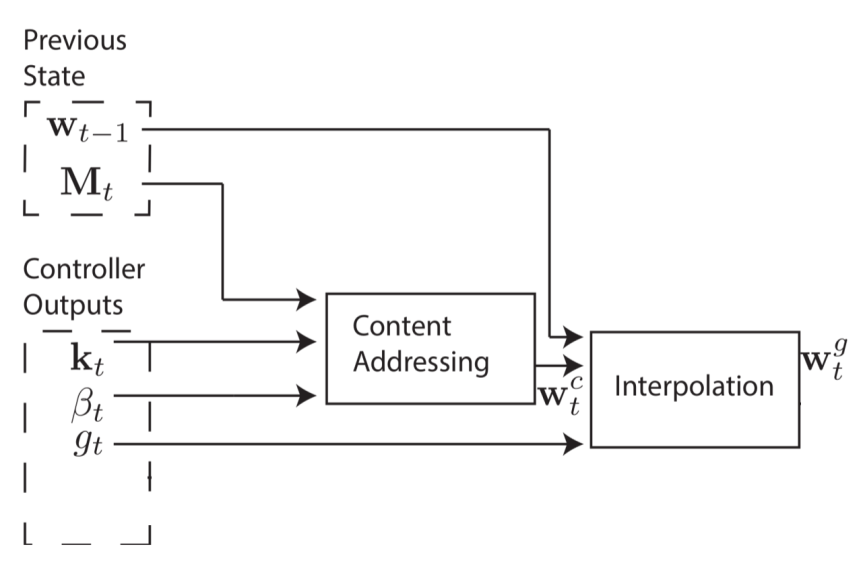
2. Shifting and Sharpening
基于地址的寻址机制既可以用做简单的 memory bank 遍历,也可以用于随机访问,通过对 weighting 的旋转位移操作来实现。如果当前 weight 全力聚焦在一个单一地址上,那么一个为 1 的旋转可以把部分焦点位移到下一个地址,一个负的位移则相反。
具体是在 Interpolation 之后进行。controller 产生的 shift weighting $s_t$ 定义了所有允许的整数位移值上的归一化分布。如果 -1 到 1 间的位移是被允许的,那么 $s_t$ 就有三个对应位移值 -1,0,1 上的概率分布。最简单是用 softmax 来预测 shift weighting,不过这里用了另一种方法,controller 产生一个 single scalar 表示均匀分布的下界(the lower bound of a width one uniform distribution over shifts),也就是如果 shift scalar=6.7,那么 $s_t(6)=0.3$,$s_t(7)=0.7$,剩下的 $s_t(i)$ 都是 0。
Shift attention:
$$\hat w_t \leftarrow \sum^{R-1}_{j=0}w^g_t(j)s_t(i-j)$$
$s_t$ 其实相当于一个 convolution filter,每一个元素表示当前位置和对应位置的相关程度,像是定义了一个滑动窗里的权重,shift attention 将滑动窗里的 vector 做加权平均。
如果位移权重不是 sharp 的,也就是说权重分布相对均匀,那么这个卷积操作会使权重随时间变化更加发散。例如,如果给 -1,0,1 的对应的权重 0.1,0.8 和 0.1,旋转位移就会将聚焦在一个点上的权重轻微分散到三个点上。
controller 还会给出一个标量 $\gamma_t$ 用来 sharpen 最终的权重,作用和之前讲过的 $\beta_t$ 差不多,值越大权重大的越突出。
Sharpening:
$$w_t(i) \leftarrow {\hat w_t(i)\gamma_t \over \sum_j \hat w_t(i)\gamma_t}$$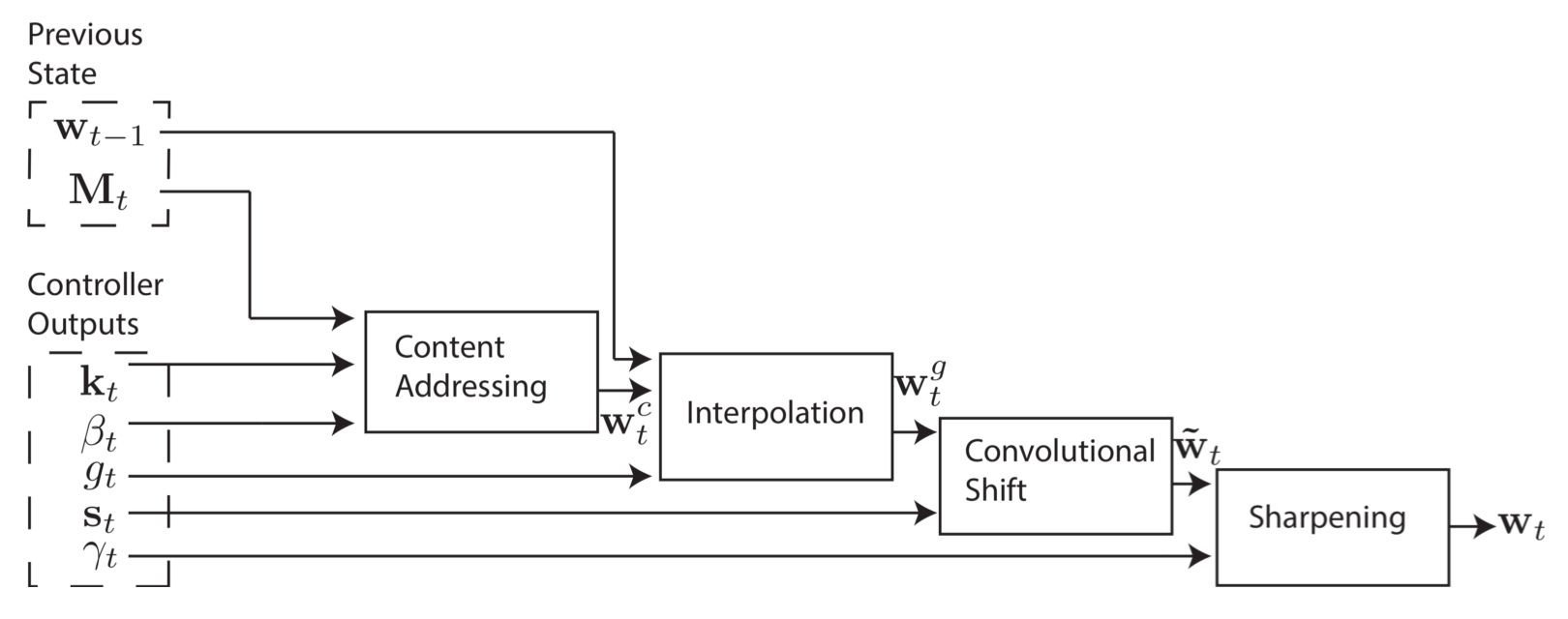
结合权重插值(weighting interpolation)、内容寻址(content-based addressing)和地址寻址(location-based addressing)的寻址系统可以在三种补充模式下工作:
- 权重可以完全由 content-based addressing 来自主选择而不受 location system 的影响
- 由 content-based addressing 产生的权重可以被选择然后进行位移。这使得 focus 能够跳跃到通过内容寻址产生的地址附近而不是具体一个点。在计算方面,这使得 head 可以访问一个连续的数据块,然后访问这个块中的特定数据
- 来自上一个时刻的权重可以在没有任何 content-based addressing 的输入的情况下被旋转,以便权重可以以相同的时间间隔连续地访问一个地址序列(allows the weighting to iterate through a sequence of addresses by advancing the same distance at each time-step)。
Summary
input 被 controller 加工产生 key vector 和一些中间变量,基于 key vector 和 memory bank 里的记忆向量的相似程度,用 attention 机制将 memory 检索结果转化成 vector 返回给读操作;基于 controller 加工后的外界输入,把一些信息写到 memory 里面,实现更新 memory 的效果(擦除+更新,都需要 weight vector 来确定 memory vector 的权重,权重由 content-base+location-base 产生,表示输入与记忆的相似程度,记忆与记忆的相似程度)。
NTM 架构有三个 free parameters:
- size of memory
- number of read and write heads
- range of allowed location shifts
但最重要的选择还是用作 controller 的网络模型。来探讨下 recurrent 和 feedforward network 的选择
- 递归网络像 LSTM 拥有自己的 internal memory,可以对矩阵中更大的存储器起到补充作用。想象 controller 是 CPU,memory 是 RAM,那么 RN 里的 hidden activations 相当于处理器的寄存器(rigisters),允许 controller 跨时间操作时可以共享信息
- 前馈网络 FN 可以通过每一时刻读写同一个记忆地址来模拟 RN,在网络操作上有更大透明度,读写 memory matrix 的模式比 RNN 的中间状态更容易解释。但局限是并行 read/write heads 的数量有限,在 NTM 计算时会成为瓶颈。单个 read head 在每个时刻只能对单个 memory vector 进行一元变换,而两个 read heads 可以进行二元向量变换,以此类推。递归控制器能够存储上一时刻的读出的向量,不会受到这个限制。
Differentiable Neural Computer(DNC)
NTM 的第二个版本。更加复杂一些吧。
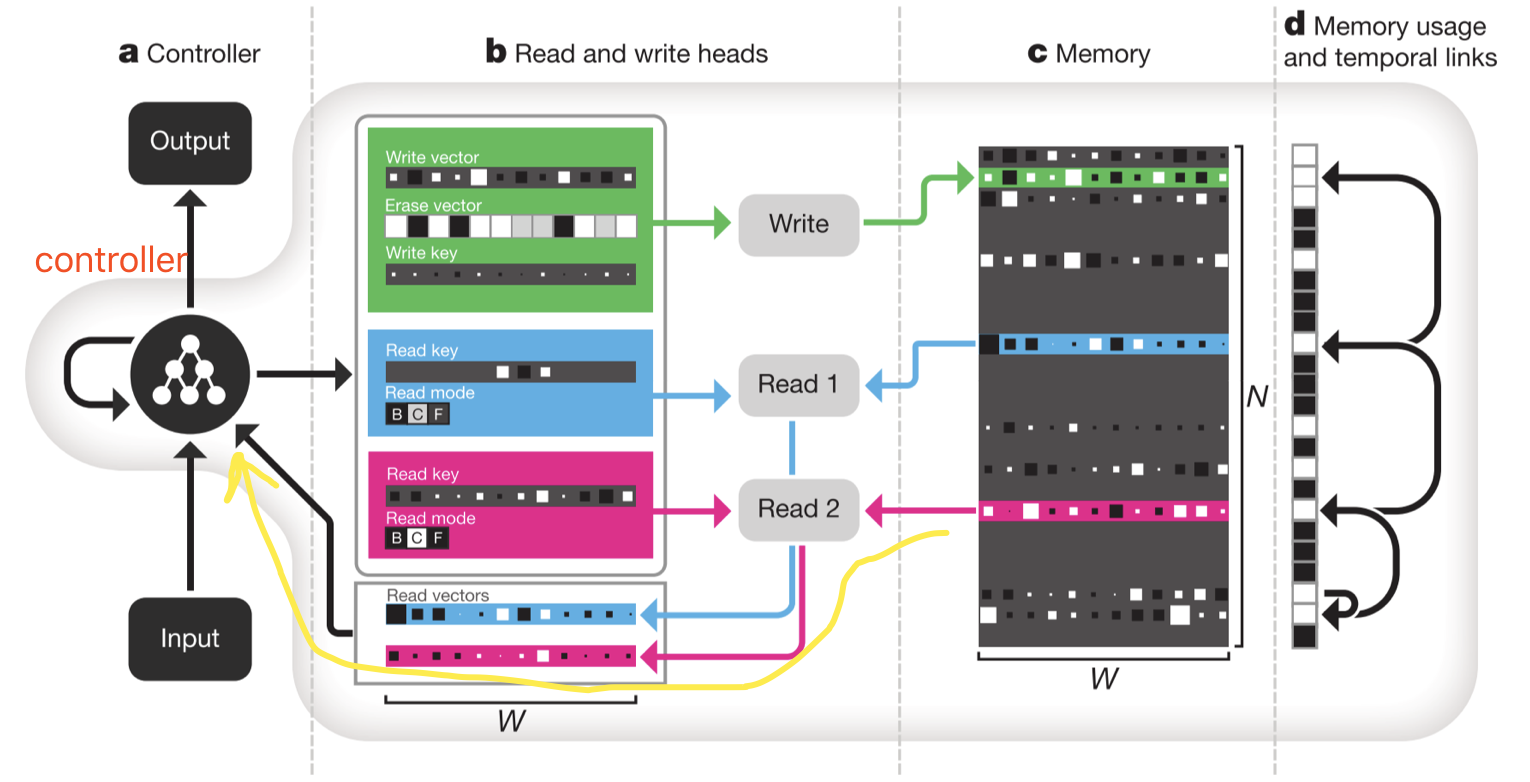
和 NTM 一样,controller 由若干个神经网络组成,负责和输入、输出交互,产生一些中间变量(又叫 interface parameter)。根据这些中间变量,可以进行 memory 的读写操作,注意这里是 先写再读! 绿色的方块表示写操作,可以看到先是会释放某些区域的记忆,然后分配记忆,写入东西,完成后输出,表示 done,可以重新分配记忆了,然后交替,整个是动态分配的过程。
紫色的方块表示读操作,更新完 memory,会从更新过的 memory 里定位和读取信息。有多个互相独立的 read model,互相独立的来从 memory 里读取信息并拼到一起,可以从各个角度来衡量信息的有用程度。
记忆区的右边(d Memory usage and temporal links)有一个附加的链表,追踪上面的箭头能够“回想”最近输入和输出的过程。
和 Seq2seq 类比一下,图中 controller 指向自己的箭头其实相当于 RNN decoder里的 RNN state vector,黄线从 memory 到 controller 的路径其实相当于 attention 提取的 context vector。
Architecture
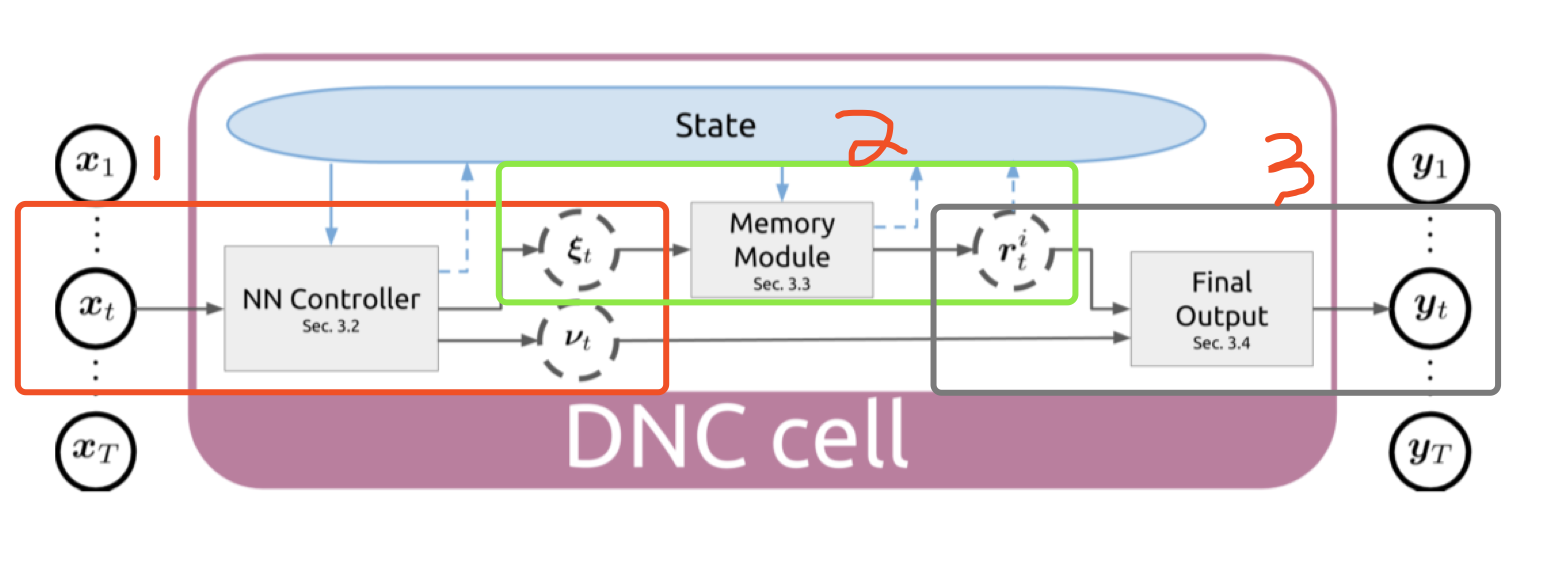
梳理一下,有三大部分:
- Controller 产生 interface parameters 和 output parameters
$x_t=[x_t;r^1_{t-1};…;r^R_{t-1}]$
$(\xi t, v_t)=NNC([x_1;…;x_t];\theta)$ - 对 memory 的操作,先写再读
Content-based writing and reading weight
History-based writing weight => final writing weights
History-based reading weight => final reading weights - Memory 结果(类比对话系统里的上下文 context vector)和 controller 产生的 $v_t$(类比RNN decoder 的 state vector)拼到一起产生最后的输出
$y_t=W_r[r^1_t,…r^R_t]+v_t$
完整的连续输入的结构图如下,上一时刻读的信息也会作为输入放到 controller 里做预测,也就是说除了 input,controller 还会用到历史信息。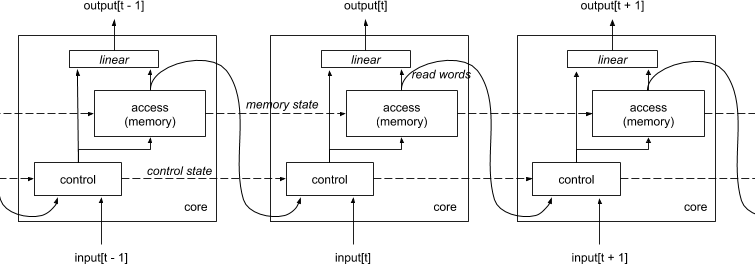
Details
下面说一下 memory 读写操作的细节。沿着下图走一遍,图中六角形部分都是控制器的输出也就是 interface parameter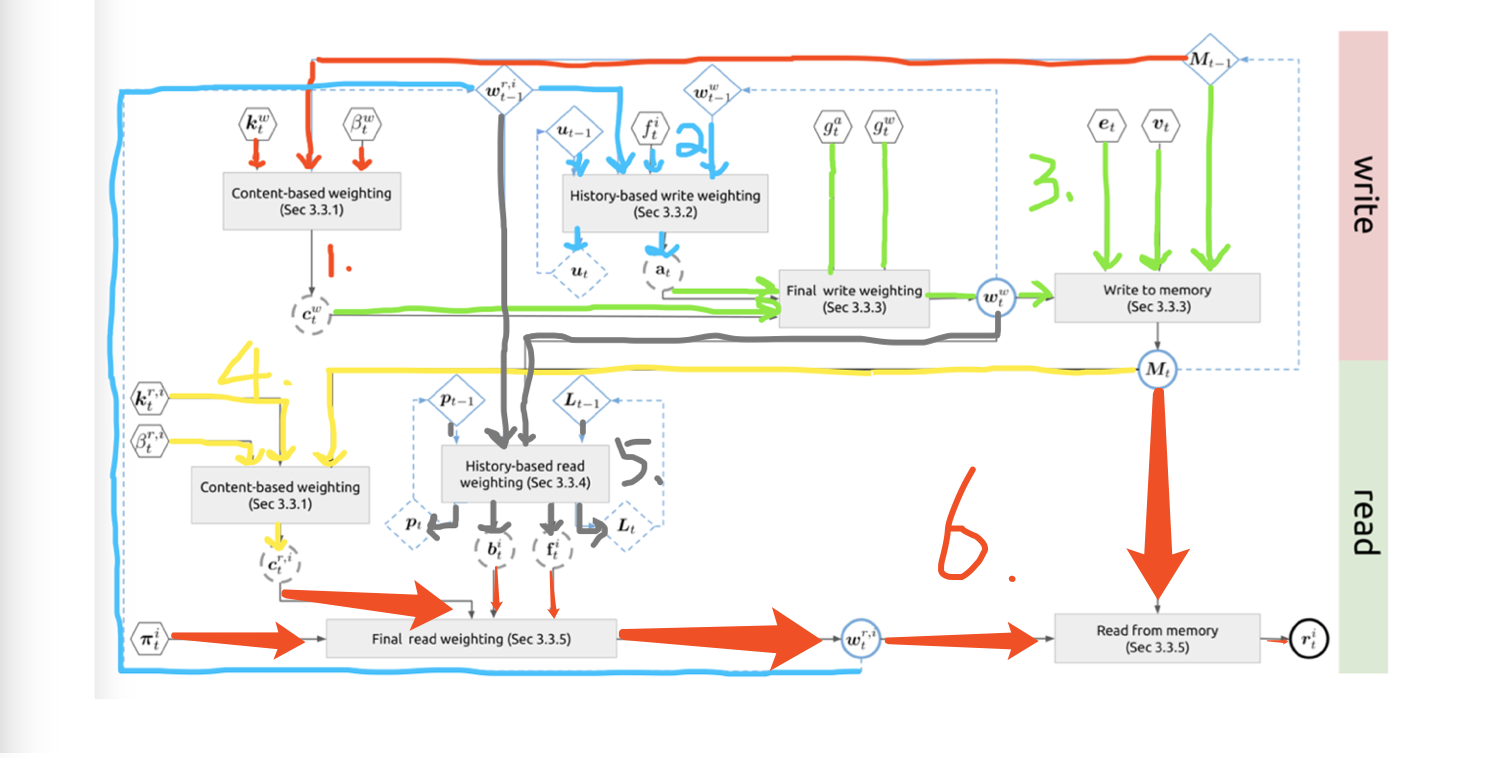
1. Content-based weighting for memory write
这一部分 $c^w_t$ 和 NMT.v1 相同。D 是相似度函数,可以取 cosine similarity; $\beta$ 是 concentration parameter,表示 key strength,是大于 1 的 scalar
$$C(M_{t-1}, k^w_t, \beta^w_t)[i]={exp(D(k^w_t, M_{t-1}[i, ·])\beta_t^w \over \sum_j exp(D(k^w_t, M_{t-1}[j,·])\beta^w_t))}$$
2. History-based write weighting(Dynamic memory allocation)
对应 NTM 的 remove 和 add 操作。每一个存储单元都是一个等长 vector,里面有若干个 element,只要 element 没有全部被占用,就可以写入新数据。如果被完全占用了,也可以通过一定方法将存储单元释放。
Controller 有三种选择:
- 不写
- 写 & 写到新分配的位置(未使用过的/最新释放的存储单元)
- 写 & 写到内容相似且还没有被完全占用的存储单元
也就是更新这个存储单元的信息
如果所有存储空间都用完了,那么控制器必须释放空间才可以进行写操作。每一个时刻的写操作完成后,位置信息会和 L 矩阵也就是 links of association 连接起来,记录信息存储的顺序。
- memory retention vector: $\psi_t = \prod^R_{i=1}(1-f^i_t \omega^{r,i}_{t-1})$
$\omega^{w,i}_{t-1}$ 是上一时刻的 write weights,$f^i_t$ 是 controller 产生的 free gates,决定最近读取的位置要不要被释放。i 是 read head 的 index。$\psi_t \in [0,1]$ 也就是 memory retention vector,表示每个位置上有多少信息被保留下来 - usage vector: $u_t=(u_{t-1}+\omega^w_{t-1}-(u_{t-1}⊙\omega_{t-1}^w))⊙ \psi_t$
$u_t$ 是 t 时刻的 usage vector,衡量每一个 memory vector 最近被用到的程度,如果很久没用&需要腾地方,就会优先把它给踢掉
$u_t$ 被 $\psi_t$ 限制,在 0-1 之间,⊙ 表示 element-wise 乘法 - least used location: $\phi_t=SortIndicesAscending(u_t)$
升序排序,于是 $\phi_t[1]$ 表示最少使用到的位置 - allocation weighting: $a_t[\phi_t[j]]=(1-u_t[\phi_t[j]])\prod^{j-1}_{i=1}u_t[\phi_t[j]]$
最近读取的 memory 在更新 memory 的时候有更大的权重
$a_t$ 是 allocation weighting,提供写操作的新的位置,如果所有的 u 都是 1,那么 $a_t=0$,必须先释放存储空间才能够分配空间
3. Final write weight
Usage attention 和 content attention 通过 gate 线性组合, gate 也是 interface parameter, 再做后续 filter。
- $\omega^w_t=g^w_t[g^a_ta_t+(1-g^a_t)c^w_t]$
$g^a_t$ 是线性组合的 allocation gate,$g^w_t$是 write gate,如果 write gate 是 0,那么啥都不写 - $M_t=M_{t-1}⊙(E-\omega^w_te^T_t)+\omega^w_tv^T_t = M_{t-1}-M_{t-1}⊙\omega^w_te^T_t+\omega^w_tv^T_t$
Memory writes,改变 t-1 时刻的 memory bank
4. Content-based weighting for memory read
$$C(M_t, k^{r,i}_t,\beta^{r,i}_t)[k]={exp(D(k^{r,i}_t, M_t[k, ·])\beta^{r,i}_t) \over \sum_j exp(D(k^{r,i}_t,M_t[j, ·])\beta^{r,i}_t)}$$
总共读 R 次($R\ge 1,$超参数),从更新过以后的 memory $M_t$ 里读信息
5. History-based reading weights
通过有时间信息的历史记录(temporal links),和 content-based read 挑出来的 C,进一步挑选出不直接相关但历史上有间接联系的 memory vector。举个例子理解一下,t 时刻的 input 通过内容的相似程度定位到了第 5 个 memory vector,然后 L 矩阵通过写操作的历史记录,发现第 5 个 vector 和第 2,4,6 个 vector 非常相关,所以尽管 t 时刻的 input 和 vector 2,4,6 在这一时刻表面上不相关,但有了第 5 个 vector 作为中介找到了 2,4,6,就有了间接关系,这可以通过 f, b 挑选出来。
$p_0=0$
$p_t=(1-\sum^N_{i=1}\omega^w_t[i])p_{t-1}+\omega^w_t$
$L_0[i,j]=0 \ \ \forall i,j $
$L_t[i,i]=0 \ \ \forall i $
$L_t[i,j]=(1-\omega^w_t[i]-\omega^w_t[j])L_{t-1}[i,j]+\omega^w_t[i]p^w_{t-1}[j]$
$L_t[i,j]$: the degree to which location i was the location written to after location j,the rows and columns of Lt represent the weights of the temporal links going into and out from particular memory slots, respectively
每次修改存储空间时,链接矩阵都会更新,删除旧位置的链接,添加最后写入的位置的新链接。
从 L 中挑选:
- $b^i_t$ backward weighting
$b^i_t=L^T_t\omega^{r,i}_{t-1}$ - $f^i_t$ forward weighting
$f^i_t=L_t\omega^{r,i}_{t-1}$
这种 temporal links 特别适用于NLP的任务。比如一段文本以单词为单位输入喂给 DNC,每个单词输入下 memory 都会被更新,但根据 L 可以知道上一个单词都影响了哪些 memory,也就是能够去关注单词的时序关系,这对捕捉文本意义有重要作用。
6. Final read weighting
- $\omega^{r,i}_t=\pi^i_t[1]b^i_t+\pi^i_t[2]c^{r,i}_t+\pi^i_t[3]f^i_t$
$\pi^i_t$ 表示读的模式,如果 $\pi^i_t[2]$ 占主导,那么只用 content lookup,如果 $\pi^i_t[3]$ 占主导,那么就按 memory 写入的顺序来遍历,如果 $\pi^i_t[1]$ 占主导,按 memory 写入顺序反向遍历 - $r^i_t=M^T_t\omega^{r,i}_t$
Read from memory,三个 weight vector 加权相加得到最后的 weight vector,然后从更新过的 memory vector 把 memory 读出来加权平均返回给控制器
小结一下,对于读操作,控制器可以从多个位置读取记忆,可以基于内容读取,也可以基于 associative temporal links 读取(向前/向后以顺序或反序的方式回调依次读取写入的信息)。读取的信息可以用来生成问题答案或者在环境中采取的行为。
Others
controller 可以用简单的 RNN,复杂些的 LSTM,也可以用 RL。论文还举了一些 DNC 的应用例子,比如学会找最短路径、伦敦地铁的路径规划、家族树(回答 who is Freya’s maternal great uncle 这类问题)、移动块问题等。
DNC vs. NTM
DNC 是 NTM 的第二版,它改进了 NTM 的寻址机制,去掉了 index shift,更好支持了对记忆的 allocate 和 de-allocate 的功能。具体来说表现在下面几个方面:
- No index shift based addressing
NTM 是沿着磁带(或者说记忆)左右移动,而 DNC 则尝试基于输入直接在记忆中搜索给定的 vector - Can ‘allocate’ and ‘deallocate’ memory
DNC 可以分配和释放记忆。NTM 不能保证多个存储单元之间互不重叠、互不干扰(=> allocate a free space),也不能释放存储单元,这意味着不能重复使用存储单元,也就很难处理很长的序列(=> free gates used for deallocation)
另外,这种机制也很容易能将记忆中的某个区域标记为禁止访问,避免在以后意外地删除它们,这有助于优化 - Remembers recent memory use
NTM 中,序列信息只能通过连续位置的写操作来顺序保存,并回到 memory 起点将它们读出来。一旦写操作跳跃到一个很远的位置,那么跳跃前和跳跃后的存储顺序就丢失了,读操作是没办法获取的
而 DNC 有一个 temporal link matrix 记录了写操作的顺序,也就是说 DNC 有某种形式的 temporal memory,在某个瞬时记忆下 DNC 可以回想起上一步做的事,以及上一步的上一步,以此类推,也就是可以遍历由它们需要做的事组成地一个链表
参考链接
DeepMind DNC Slides
Neural Turing Machines: Perils and Promise

